有什么看似违反热力学第二定律的物理现象?
很多热力学性质都是建立在粒子数足够多(热力学极限)的基础上的,所以到小的体系就越容易出现“违反”热力学定律的现象,但实际上只需要对现有的热力学定律进一步 refine,就可以使其在小体系中也成立,而这一方法也演变成了非平衡态统计物理的一个研究方向——随机热力学,stochastic thermodynamics 回到这个问题本身,热力学第二定律的一个推论是卡诺定理,而在热力学中所学习的卡诺循环的工作介质都是自由度极大的宏观气体,现在我们将我们的视线移到小体系,来看看小体系是如何“违背”热力学定律的。说起来还是我本科的第一个课题的背景 考虑一个稀溶液,溶质是能够在溶剂的热运动碰撞下进行布朗运动的胶粒,溶液上方由可以调节的激光器提供弹簧势,其哈密顿量 ,这里 k 就是激光器的参数。现在想象一下激光器的作用,如果 k 增大,则胶粒受到激光 trap 的力增大,可运动范围实际上缩小了,反之同理,因此,k 相当于一个和体积成反比的参数。另一个在实验中可以调节的参数是溶液的温度。温度、体积,如果足够敏感,应该想到了我们接下来要做什么。也就是用这样一个 laser trapped beads 的系统设计一个(类似)卡诺循环,控制方案如图 第一阶段,温度不变,k 增大,即恒温压缩,第二阶段,温度、k 都增大,即绝热压缩,第三阶段,温度不变,k 减小,即恒温膨胀,第四阶段,温度、k 都减小,即绝热膨胀,并且温度、k 回到原始值,进入下一循环,整个过程会由于“体积”变化作功,而第三阶段和高温热源接触吸热则用于定义效率 物理图像如上,那么这样一个小体系是如何“挑战”热力学第二定律的。从上面的图 D 可以发现,过程的熵变并不完全顺着闭合的热力学估计结果,而是在这一值附近涨落。可以如此理解,大家在概统中学过大数定律,当用来估计的样本数足够多时,估计值会收敛到期望,但是现在的小体系中,样本数并不是足够多,因此估计值是有分布的,而不是退化到某一确定的值。这时,一部分样本轨道的平均值将大于卡诺极限,当然,同时也会有很多样本轨道的平均值小于卡诺极限,但总的来说,系综平均应该是保持了热力学定律的,只是分布上会打破热力学定律 这样的卡诺热机有没有什么用途。首先,它在实验上说明了小系统重新定义热力学的必要性。其次,由于宏观上的卡诺热机需要在运转周期无限长的情况下才能达到最大效率,而小系统的卡诺热机在周期相对很短的情况下,效率基本上就不变了,因此,实际应用更加方便 那么,小体系中的热力学定律要如何 refine。我们需要引入分布、熵函数(耗散函数)、并且对我们所选定的理论体系有一些要求,例如熵函数具有反演对称性,系统的状态的转移满足细致平衡条件等。之后就可以通过前向后向概率只比来给出涨落定理、Crooks 涨落定理、Jarzynski 等式等等,作为这些定理的推论,自然会有热力学第二定律,即总熵的系综平均非负,而 Jarzynski 等式通过系综平均给出了状态量自由能和过程量做功之间的等式关系,因此被广泛应用于生物物理方面的研究中,如 DNA 拉伸试验中用做功来估计自由能,同时也有很多改进,如 Stanford 的 Vijay Pande 和统计系的 Eric Bair、Giles Hooker 合作利用极大似然法改进 Crooks 涨落定理的估计效果等,第一次看到这个论文的时候还有点惊讶,因为其中有一步推导极大似然的过程和我们当时概统期末考试的题目是一样的,可能是我本科离 PRL 最近的一次了 23333 有了随机热力学的体系,也就可以理解时间之箭问题,为什么微观运动具有时间反演对称,但是到宏观层次就有了明确的时间演化方向,原因正是在于,根据涨落定理,正反向概率之比为熵函数的指数,在小体系,熵函数很小、接近于 0,可以认为正反向概率相等,而到了宏观层次,熵相对大,因此正反向概率之比非常大,也就有了明确的时间演化方向,因为我们定义了概率最大的方向就是时间的变化方向 涨落定理(不是涨落耗散定理)是热力第二的统计证明吗?董玉龙:非平衡统计物理 2——熵、耗散函数Brownian Carnot engine 查看知乎讨论


很多热力学性质都是建立在粒子数足够多(热力学极限)的基础上的,所以到小的体系就越容易出现“违反”热力学定律的现象,但实际上只需要对现有的热力学定律进一步 refine,就可以使其在小体系中也成立,而这一方法也演变成了非平衡态统计物理的一个研究方向——随机热力学,stochastic thermodynamics
回到这个问题本身,热力学第二定律的一个推论是卡诺定理,而在热力学中所学习的卡诺循环的工作介质都是自由度极大的宏观气体,现在我们将我们的视线移到小体系,来看看小体系是如何“违背”热力学定律的。说起来还是我本科的第一个课题的背景
考虑一个稀溶液,溶质是能够在溶剂的热运动碰撞下进行布朗运动的胶粒,溶液上方由可以调节的激光器提供弹簧势,其哈密顿量
,这里 k 就是激光器的参数。现在想象一下激光器的作用,如果 k 增大,则胶粒受到激光 trap 的力增大,可运动范围实际上缩小了,反之同理,因此,k 相当于一个和体积成反比的参数。另一个在实验中可以调节的参数是溶液的温度。温度、体积,如果足够敏感,应该想到了我们接下来要做什么。也就是用这样一个 laser trapped beads 的系统设计一个(类似)卡诺循环,控制方案如图
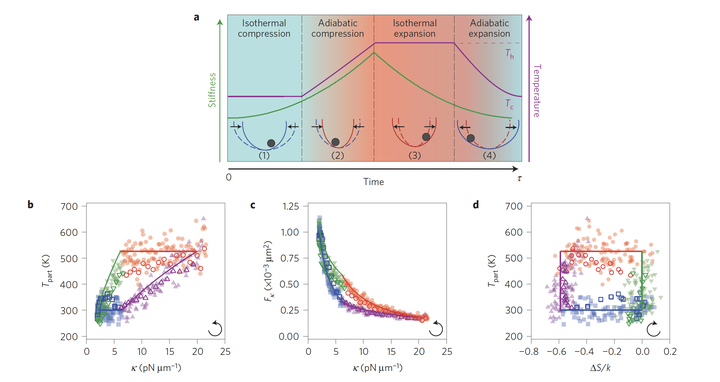
第一阶段,温度不变,k 增大,即恒温压缩,第二阶段,温度、k 都增大,即绝热压缩,第三阶段,温度不变,k 减小,即恒温膨胀,第四阶段,温度、k 都减小,即绝热膨胀,并且温度、k 回到原始值,进入下一循环,整个过程会由于“体积”变化作功,而第三阶段和高温热源接触吸热则用于定义效率
物理图像如上,那么这样一个小体系是如何“挑战”热力学第二定律的。从上面的图 D 可以发现,过程的熵变并不完全顺着闭合的热力学估计结果,而是在这一值附近涨落。可以如此理解,大家在概统中学过大数定律,当用来估计的样本数足够多时,估计值会收敛到期望,但是现在的小体系中,样本数并不是足够多,因此估计值是有分布的,而不是退化到某一确定的值。这时,一部分样本轨道的平均值将大于卡诺极限,当然,同时也会有很多样本轨道的平均值小于卡诺极限,但总的来说,系综平均应该是保持了热力学定律的,只是分布上会打破热力学定律
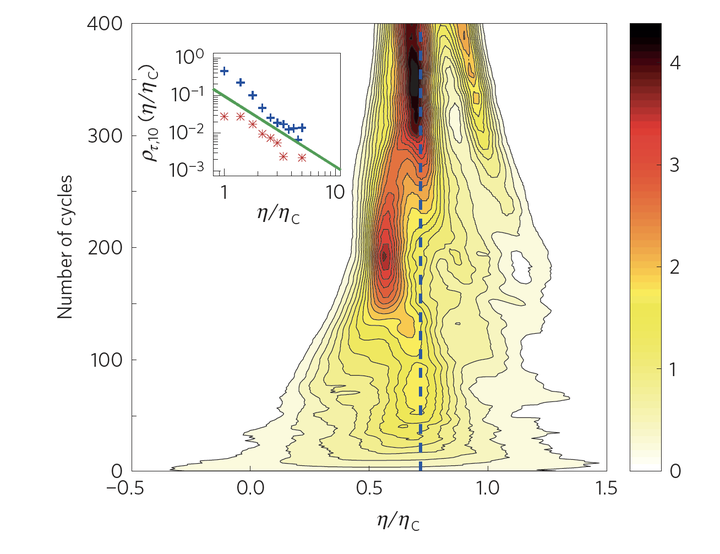
这样的卡诺热机有没有什么用途。首先,它在实验上说明了小系统重新定义热力学的必要性。其次,由于宏观上的卡诺热机需要在运转周期无限长的情况下才能达到最大效率,而小系统的卡诺热机在周期相对很短的情况下,效率基本上就不变了,因此,实际应用更加方便
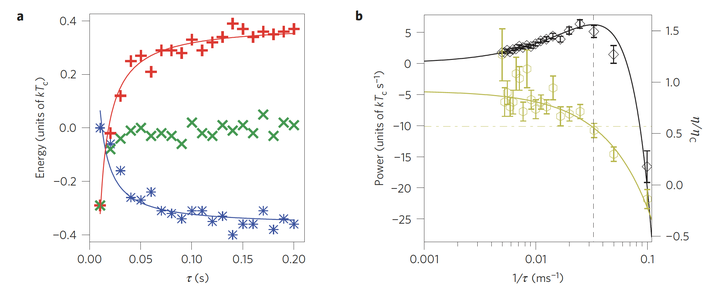
那么,小体系中的热力学定律要如何 refine。我们需要引入分布、熵函数(耗散函数)、并且对我们所选定的理论体系有一些要求,例如熵函数具有反演对称性,系统的状态的转移满足细致平衡条件等。之后就可以通过前向后向概率只比来给出涨落定理、Crooks 涨落定理、Jarzynski 等式等等,作为这些定理的推论,自然会有热力学第二定律,即总熵的系综平均非负,而 Jarzynski 等式通过系综平均给出了状态量自由能和过程量做功之间的等式关系,因此被广泛应用于生物物理方面的研究中,如 DNA 拉伸试验中用做功来估计自由能,同时也有很多改进,如 Stanford 的 Vijay Pande 和统计系的 Eric Bair、Giles Hooker 合作利用极大似然法改进 Crooks 涨落定理的估计效果等,第一次看到这个论文的时候还有点惊讶,因为其中有一步推导极大似然的过程和我们当时概统期末考试的题目是一样的,可能是我本科离 PRL 最近的一次了 23333
有了随机热力学的体系,也就可以理解时间之箭问题,为什么微观运动具有时间反演对称,但是到宏观层次就有了明确的时间演化方向,原因正是在于,根据涨落定理,正反向概率之比为熵函数的指数,在小体系,熵函数很小、接近于 0,可以认为正反向概率相等,而到了宏观层次,熵相对大,因此正反向概率之比非常大,也就有了明确的时间演化方向,因为我们定义了概率最大的方向就是时间的变化方向
涨落定理(不是涨落耗散定理)是热力第二的统计证明吗?董玉龙:非平衡统计物理 2——熵、耗散函数Brownian Carnot engine
















































