Use High School Mathematics Knowledge to Teach the “82 Rule” and its Application

Columnist: Dr. Matthew Yip (Prof. Mathematician)

The “80-20 rule” means that the first 20% of the “effort” will get the first 80% of the “return”. Using a function to express in high school, first set the function to pass (0,0), (1,1) and (0.2,0.8), and then assume it to be an exponential function, i.e., .

Substitute  and , we have , i.e., . Therefore, , where , is a function representing the “80-20 rule”.

Below is the graph of function:

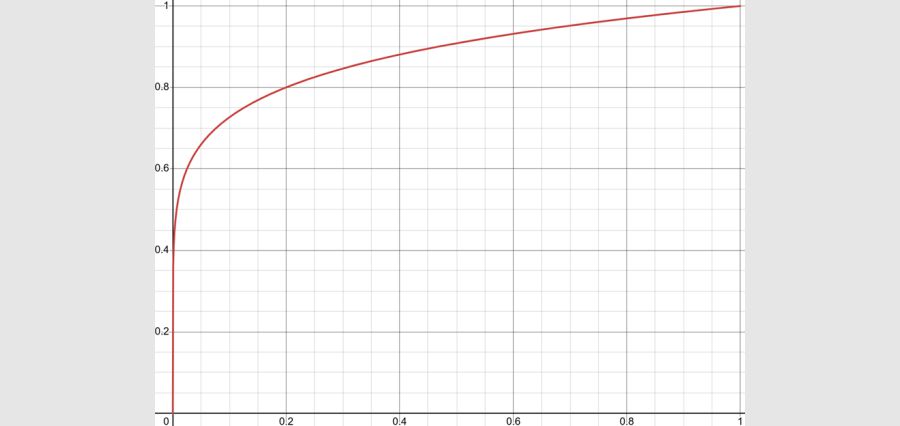
After establishing a function representing the “80-20 rule”, examples can be used to deepen students’ understanding. The following is an example:

Assume that there are 10 million people in the world who are mainly or mainly engaged in mathematics education.

Their “influence” follows the “80-20 rule”. The “influence” of the most “influential” person must account for the “influence” of all people. What percent of “power”?

We only need to substitute  to find , which means that the “influence” of the most “influential” person has exceeded 10%!

This example allows students to feel the magic of the “80-20 Rule”!

For more extensions of the “80-20 rule”, see “Fusion of “Singular Points” and the “80-20 Rule.”

The post Use High School Mathematics Knowledge to Teach the “82 Rule” and its Application appeared first on Insights Success.